BOJ 2630 - 색종이 만들기 문제풀이
문제를 읽고 이해하기
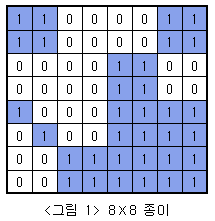
아래 <그림 1>과 같이 여러개의 정사각형칸들로 이루어진 정사각형 모양의 종이가 주어져 있고, 각 정사각형들은 하얀색으로 칠해져 있거나 파란색으로 칠해져 있다. 주어진 종이를 일정한 규칙에 따라 잘라서 다양한 크기를 가진 정사각형 모양의 하얀색 또는 파란색 색종이를 만들려고 한다.
전체 종이의 크기가 N×N(N=2^k, k는 1 이상 7 이하의 자연수) 이라면 종이를 자르는 규칙은 다음과 같다.
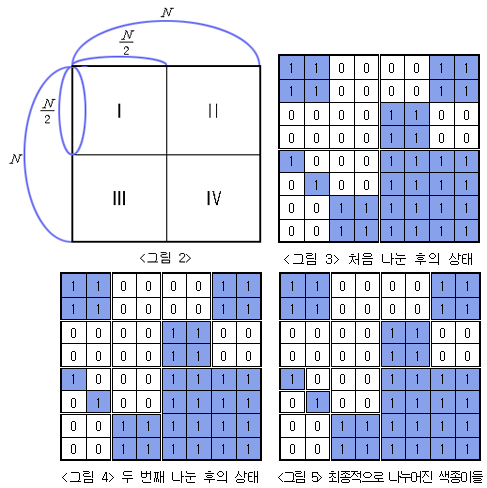
전체 종이가 모두 같은 색으로 칠해져 있지 않으면 가로와 세로로 중간 부분을 잘라서 <그림 2>의 I, II, III, IV와 같이 똑같은 크기의 네 개의 N/2 × N/2색종이로 나눈다. 나누어진 종이 I, II, III, IV 각각에 대해서도 앞에서와 마찬가지로 모두 같은 색으로 칠해져 있지 않으면 같은 방법으로 똑같은 크기의 네 개의 색종이로 나눈다. 이와 같은 과정을 잘라진 종이가 모두 하얀색 또는 모두 파란색으로 칠해져 있거나, 하나의 정사각형 칸이 되어 더 이상 자를 수 없을 때까지 반복한다.
위와 같은 규칙에 따라 잘랐을 때 <그림 3>은 <그림 1>의 종이를 처음 나눈 후의 상태를, <그림 4>는 두 번째 나눈 후의 상태를, <그림 5>는 최종적으로 만들어진 다양한 크기의 9장의 하얀색 색종이와 7장의 파란색 색종이를 보여주고 있다.
입력으로 주어진 종이의 한 변의 길이 N과 각 정사각형칸의 색(하얀색 또는 파란색)이 주어질 때 잘라진 하얀색 색종이와 파란색 색종이의 개수를 구하는 프로그램을 작성하시오.
재정의와 추상화
문제에서 말한 '일정한 규칙'은 '똑같은 크기'의 네 개의 N/2 × N/2 색종이로 나눈다고 되어있다. 이는 분할 정복의 구성 요소 중, 분할을 수행할 자연스러운 방법을 얘기한다. 즉, 색종이가 모두 같은 색이 아닐 경우, 똑같은 크기로 4등분 하고, 그 하나 하나의 등분에 대하여 똑같이 분할을 수행한다. 그러다가 해당 등분의 색이 모두 같을 경우 등분을 중지하고 해당 등분의 색의 변수를 +1한다.
계획 세우기
색종이 한 변의 최대 길이는 2^7 = 128이다. 가로 128, 세로 128을 크기로 하는 배열 rectangle을 선언한다. 그리고, 사용자로부터 한 변의 길이인 N을 받고, 이중 for문을 통해 값을 모두 받는다.
그리고 색깔별 색종이 수를 저장할 int color[2] = { 0, };를 선언한다. 꼭 0으로 초기화를 해줘야 카운트를 할 수 있다. color[0]은 하얀색 색종이의 개수를 의미하고, color[1]은 파란색 색종이 수를 의미한다.
그리고 시작 좌표, 한 변의 길이를 매개변수로 가지는 go(pair<int, int> coord, int side)라는 함수를 만든다. coord 매개변수는 시작점의 좌표를 나타내며, side는 한 변의 길이를 말한다.
go 함수는 coord의 좌표에 대해 가로 side, 세로 side 만큼만 색상을 조사한다. 조사하는 도중 rectangle[coord.first][coord.second] (주어진 범위의 첫 번째 요소)와 다른 색상이 있을 경우 즉시 탐색을 종료하여 네 등분하여 각각의 등분에 대해 go() 함수를 실행한다. (재귀)
만약 3번 과정에서 다른 색상이 발견되지 않을 경우 color[rectangle[coord.first][coord.second]]++;를 시행하여 색종이 수를 하나 카운트한다. rectangle[coord.first][coord.second]는 해당 등분의 색종이 색상(0 : 하얀색, 1 : 파란색)을 의미한다.
계획 검증하기
시간 복잡도 검사
재귀를 진행할 때마다 다른 색상이 있는지 검사해야 하므로 side * side 배열을 검사한다. 중간에 다른 색상이 있을 경우 탐색을 종료할 수 있으므로 정확한 시간 복잡도를 계산할 수는 없다. 그러나, 최대로 시간이 걸릴 수 있는 경우를 넘어서, go() 한 번 수행하는 대에 O(N^2)의 시간이 걸린다고 가정, O(N^2) * (N번 수행한다고 가정) = O(N^3) 이렇게 하여도 N의 최대값 128^3 = 2097152 밖에 걸리지 않으므로 시간 초과는 걸리지 않을 것이라고 판단하였다.
코드 작성
#include <iostream>
#include <utility>
using namespace std;
int rectangle[128][128] = { -1, };
int color[2] = { 0, };
void go(pair<int, int> coord, int side) {
bool diffFlag = false; // 다른 수가 있으면 true가 되는 flag
for (int i = 0; i < side; i++) {
for (int k = 0; k < side; k++) {
if (rectangle[coord.first][coord.second] != rectangle[coord.first + i][coord.second + k]) {
diffFlag = true;
break;
}
}
if (diffFlag)
break;
}
if (!diffFlag) {
color[rectangle[coord.first][coord.second]]++;
return;
}
go(make_pair(coord.first + 0, coord.second + 0), side / 2);
go(make_pair(coord.first + side / 2, coord.second + 0), side / 2);
go(make_pair(coord.first + 0, coord.second + side / 2), side / 2);
go(make_pair(coord.first + side / 2, coord.second + side / 2), side / 2);
}
int main() {
int N;
cin.sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> N;
for (int i = 0; i < N; i++) {
for (int k = 0; k < N; k++)
cin >> rectangle[i][k];
}
go(make_pair(0, 0), N);
for (int i = 0; i < 2; i++)
cout << color[i] << '\n';
return 0;
}회고하기
go()의 재귀를 처리할 때, 4등분 한 rectangle을 어떻게 각각 전달할지에 대해서 생각을 하느라 시간을 많이 잡아먹었던 것 같다. 다음번에 이러한 등분 유형이 나오면 시작 지점 좌표와 한 변의 길이를 전달하도록 하자.
'알고리즘 > 문제풀이' 카테고리의 다른 글
| BOJ 1427 - 소트인사이드 문제풀이 (0) | 2020.03.25 |
|---|---|
| BOJ 1181 - 단어 정렬 문제풀이 (0) | 2020.03.25 |
| BOJ 1026 - 보물 문제풀이 (0) | 2020.03.25 |
| BOJ 11286 - 절댓값 힙 문제풀이 (0) | 2020.03.19 |
| BOJ 1010 - 다리 놓기 문제풀이 (0) | 2020.03.19 |
댓글
이 글 공유하기
다른 글
-
BOJ 1181 - 단어 정렬 문제풀이
BOJ 1181 - 단어 정렬 문제풀이
2020.03.25 -
BOJ 1026 - 보물 문제풀이
BOJ 1026 - 보물 문제풀이
2020.03.25 -
BOJ 11286 - 절댓값 힙 문제풀이
BOJ 11286 - 절댓값 힙 문제풀이
2020.03.19 -
BOJ 1010 - 다리 놓기 문제풀이
BOJ 1010 - 다리 놓기 문제풀이
2020.03.19