BOJ 1520 - 내리막 길 문제풀이
문제를 읽고 이해하기
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으며, 각 지점 사이의 이동은 지도에서 상하좌우 이웃한 곳끼리만 가능하다.

현재 제일 왼쪽 위 칸이 나타내는 지점에 있는 세준이는 제일 오른쪽 아래 칸이 나타내는 지점으로 가려고 한다. 그런데 가능한 힘을 적게 들이고 싶어 항상 높이가 더 낮은 지점으로만 이동하여 목표 지점까지 가고자 한다. 위와 같은 지도에서는 다음과 같은 세 가지 경로가 가능하다.
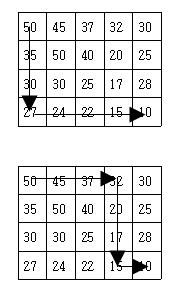
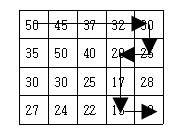
지도가 주어질 때 이와 같이 제일 왼쪽 위 지점에서 출발하여 제일 오른쪽 아래 지점까지 항상 내리막길로만 이동하는 경로의 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 지도의 세로의 크기 M과 가로의 크기 N이 빈칸을 사이에 두고 주어진다. 이어 다음 M개 줄에 걸쳐 한 줄에 N개씩 위에서부터 차례로 각 지점의 높이가 빈 칸을 사이에 두고 주어진다. M과 N은 각각 500이하의 자연수이고, 각 지점의 높이는 10000이하의 자연수이다.
출력
첫째 줄에 이동 가능한 경로의 수 H를 출력한다. 모든 입력에 대하여 H는 10억 이하의 음이 아닌 정수이다.
재정의와 추상화
DFS + DP
이 문제를 한 마디로 DFS 구현에 DP가 추가된 것이라고 말할 수 있다. 처음 이 문제를 접할 때 DFS로만 접근을 시도했는데, 그 방법으로는 답이 다르게 나왔다.
그 이유를 문제에 나온 예제 이미지를 보고 파악할 수 있었다.


첫 번째 사진과 두 번째 사진을 보자면, 17에서 20으로 가는 동선이 겹친다. 만약 첫 번째 사진의 동선을 먼저 DFS가 처리했다면, 두 번째 사진의 동선에서 17 > 15 > 10 으로 가는 동선은 이미 왔던 곳(check[y][x]가 true인 곳)이므로 더 이상 진행하지 않게 된다.
이 문제를 해결하기 위해 DP를 사용했다. 17이 적혀있는 위치에서 종착점(10)으로 가는 동선은 이미 첫 번째 사진에서 갔다 왔으므로 똑같은 루트를 한 번 더 가는 것은 시간 낭비이다. 따라서 DP(동적 계획법)를 이용해 해당 위치에서 종착점까지 가는 루트의 개수를 저장해놓고 만약 재방문했을 시 O(1)로 값을 리턴하게 한다.
코드 작성
// DFS 중심 풀이 (초기점부터 종착점까지 순차적으로 재귀하는 DFS의 원리에 중점)
#include <iostream>
using namespace std;
typedef struct {
int y, x;
} Position;
Position pos[4] = { {1, 0}, {0, 1}, {-1, 0}, {0, -1} };
int arr[500][500];
bool check[500][500];
int dp[500][500];
int m, n;
bool isInside(int y, int x) {
return y >= 0 && y < m && x >= 0 && x < n;
}
int dfs(int y, int x) {
if (y == m - 1 && x == n - 1)
return 1;
check[y][x] = true;
auto & ref = dp[y][x];
for(auto & p : pos) {
int next_y = y + p.y;
int next_x = x + p.x;
if (isInside(next_y, next_x) && arr[y][x] > arr[next_y][next_x] && !check[next_y][next_x])
ref += dfs(next_y, next_x);
else if (isInside(next_y, next_x) && arr[y][x] > arr[next_y][next_x] && check[next_y][next_x])
ref += dp[next_y][next_x];
}
return ref;
}
int main() {
cin.sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> m >> n;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> arr[i][j];
}
}
dfs(0, 0);
cout << dp[0][0];
return 0;
}// DP 중심 풀이 (Top-down 재귀에 중점)
#include <iostream>
using namespace std;
typedef struct {
int y, x;
} Position;
Position pos[4] = { {1, 0}, {0, 1}, {-1, 0}, {0, -1} };
int arr[500][500];
bool check[500][500];
int dp[500][500];
int m, n;
bool isInside(int y, int x) {
return y >= 0 && y < m && x >= 0 && x < n;
}
int dfs(int y, int x) {
if (y == 0 && x == 0)
return 1;
check[y][x] = true;
auto & ref = dp[y][x];
for(auto & p : pos) {
int next_y = y + p.y;
int next_x = x + p.x;
if (isInside(next_y, next_x) && arr[y][x] < arr[next_y][next_x] && !check[next_y][next_x])
ref += dfs(next_y, next_x);
else if (isInside(next_y, next_x) && arr[y][x] < arr[next_y][next_x] && check[next_y][next_x])
ref += dp[next_y][next_x];
}
return ref;
}
int main() {
cin.sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> m >> n;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> arr[i][j];
}
}
dfs(m - 1, n - 1);
cout << dp[m - 1][n - 1];
return 0;
}'알고리즘 > 문제풀이' 카테고리의 다른 글
| BOJ 7579 - 앱 문제풀이 (0) | 2020.04.18 |
|---|---|
| BOJ 12852 - 1로 만들기 2 문제풀이 (0) | 2020.04.18 |
| 4월 17일 공부 계획 (0) | 2020.04.15 |
| BOJ 11049 - 행렬 곱셈 순서 문제풀이 (0) | 2020.04.14 |
| BOJ 10816 - 숫자 카드 2 문제풀이 (0) | 2020.04.11 |
댓글
이 글 공유하기
다른 글
-
BOJ 7579 - 앱 문제풀이
BOJ 7579 - 앱 문제풀이
2020.04.18 -
BOJ 12852 - 1로 만들기 2 문제풀이
BOJ 12852 - 1로 만들기 2 문제풀이
2020.04.18 -
4월 17일 공부 계획
4월 17일 공부 계획
2020.04.15 -
BOJ 11049 - 행렬 곱셈 순서 문제풀이
BOJ 11049 - 행렬 곱셈 순서 문제풀이
2020.04.14